Πίνακας περιεχομένων:
- Σύνοψη Βημάτων για Παράγοντα Τετραγωνικά Τριώνυμα
- Το μάθημα θα περιλαμβάνει τους ακόλουθους έξι τύπους factoring:
Βίντεο: Πώς υπολογίζετε το Trino Ials;
2024 Συγγραφέας: Stanley Ellington | [email protected]. Τελευταία τροποποίηση: 2023-12-16 00:15
Προς το παράγοντας ένα τριώνυμος με τη μορφή x2 + bx + c, βρείτε δύο ακέραιους αριθμούς, τον r και τον s, των οποίων το γινόμενο είναι c και το άθροισμα b. Ξαναγράψτε το τριώνυμος ως x2 + rx + sx + c και στη συνέχεια χρησιμοποιήστε την ομαδοποίηση και την ιδιότητα διανομής to παράγοντας το πολυώνυμο. Το αποτέλεσμα παράγοντες θα είναι (x + r) και (x + s).
Λοιπόν, πώς συνυπολογίζετε τα τετραγωνικά τριώνυμα;
Σύνοψη Βημάτων για Παράγοντα Τετραγωνικά Τριώνυμα
- Αφαιρέστε τους κοινούς παράγοντες αν είναι δυνατόν.
- Αν ο συντελεστής του x2 ο όρος είναι 1, λοιπόν. Χ2 + bx + c = (x + n)(x + m), όπου n και m. · Πολλαπλασιάστε για να δώσετε γ. · Προσθήκη για να δώσει β.
- Αν ο συντελεστής του x2 ο όρος δεν είναι 1, τότε χρησιμοποιήστε ένα από τα δύο. Guess-and Check. Να αναφέρετε τους συντελεστές του συντελεστή του x2 όρος.
Στη συνέχεια, το ερώτημα είναι, γιατί είναι τόσο δύσκολο το factoring; Factoring είναι πιο δύσκολο από τον πολλαπλασιασμό γιατί δεν είναι τόσο μηχανικό. Πολλές φορές περιλαμβάνει εικασίες ή δοκιμές και λάθη. Επίσης, μπορεί να είναι πιο σκληρό γιατί μερικές φορές τα πράγματα ακυρώνονται όταν πολλαπλασιάζονται. Για παράδειγμα, εάν σας ζητήθηκε να πολλαπλασιάσετε (x+2)(x 2-2x+4), θα έπαιρνες x 3+8.
Επίσης το ερώτημα είναι ποιες είναι οι μέθοδοι factoring;
Το μάθημα θα περιλαμβάνει τους ακόλουθους έξι τύπους factoring:
- Ομάδα #1: Μεγαλύτερος κοινός παράγοντας.
- Ομάδα #2: Ομαδοποίηση.
- Ομάδα #3: Διαφορά σε δύο τετράγωνα.
- Ομάδα #4: Άθροισμα ή διαφορά σε δύο κύβους.
- Ομάδα #5: Τριώνυμα.
- Ομάδα #6: Γενικά Trinomials.
Ποιοι είναι οι συντελεστές του 36;
Παράγοντες 36 : 1, 2, 3, 4, 6, 9, 12, 18, 36 . Πρωταρχική παραγοντοποίηση: 36 = 2 x 2 x 3 x 3, που μπορεί επίσης να γραφτεί 36 = 2² x 3². Από √ 36 = 6, ακέραιος αριθμός, 36 είναι τέλειο τετράγωνο.
Συνιστάται:
Πώς υπολογίζετε το εύρος μισθών;
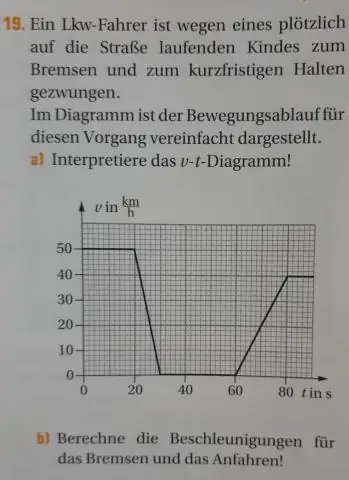
Αφαιρέστε το ελάχιστο από το μέγιστο. Αυτό είναι το εύρος. Στο παράδειγμα, 500.000 μείον 350.000 ισούται με 150.000. Διαιρέστε το εύρος με το ελάχιστο για να βρείτε το εύρος εύρους
Τι είναι το πλεόνασμα καταναλωτή και πώς το υπολογίζετε;
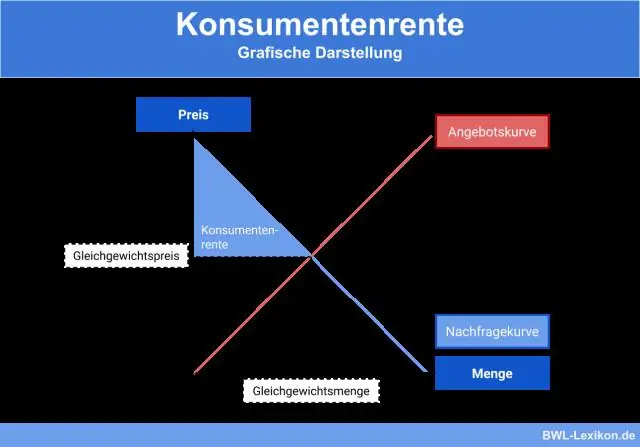
Πώς να υπολογίσετε το πλεόνασμα καταναλωτή. Σε αυτό το γράφημα, το πλεόνασμα του καταναλωτή είναι ίσο με το 1/2 βασικό ύψος. Η τιμή αγοράς είναι 18 $ με ζητούμενη ποσότητα στις 20 μονάδες (αυτό που τελικά πληρώνει ο καταναλωτής), ενώ 30 $ είναι η μέγιστη τιμή που κάποιος είναι διατεθειμένος να πληρώσει για μια μονάδα. Η βάση είναι $ 20
Πώς υπολογίζετε τη μέθοδο FIFO;
Για να υπολογίσετε το FIFO (First-In, First Out) καθορίστε το κόστος του παλαιότερου αποθέματός σας και πολλαπλασιάστε το κόστος με το ποσό του πωληθέντος αποθέματος, ενώ για να υπολογίσετε το LIFO (Last-in, First-Out) καθορίστε το κόστος του πιο πρόσφατου αποθέματός σας και πολλαπλασιάστε το με το ποσό των αποθεμάτων που πωλήθηκαν
Πώς υπολογίζετε ρευστά απεριόριστα καθαρά περιουσιακά στοιχεία;
Μήνες υγρών απεριόριστων καθαρών περιουσιακών στοιχείων (LUNA) Υπολογίστε τα ρευστά απεριόριστα καθαρά περιουσιακά στοιχεία ή LUNA σύμφωνα με το διάγραμμα εδώ και διαιρέστε αυτόν τον αριθμό με τον αριθμό μηνιαίων δαπανών σας για να λάβετε Μήνες υγρών απεριόριστων καθαρών περιουσιακών στοιχείων
Πώς υπολογίζετε τα κοινά μονοώνυμα;
Για να βρείτε τον μεγαλύτερο κοινό παράγοντα (GCF) μεταξύ των μονονομίων, πάρτε κάθε μονοώνιο και γράψτε τον πρωταρχικό παράγοντα. Στη συνέχεια, προσδιορίστε τους κοινούς παράγοντες σε κάθε μονοώνυμο και πολλαπλασιάστε αυτούς τους κοινούς παράγοντες μαζί. Μπαμ! Το GCF