
- Συγγραφέας Stanley Ellington ellington@answers-business.com.
- Public 2023-12-16 00:15.
- Τελευταία τροποποίηση 2025-01-22 15:56.
Τι είναι το φθίνον οριακό προϊόν ; Ορισμός: Μια αύξηση σε μία είσοδο ενώ οι άλλες εισροές διατηρούνται σταθερές θα οδηγήσει σε αύξηση παραγωγή . Μετά από ένα ορισμένο σημείο, το παραγωγή μπορεί να σταματήσει να αυξάνεται ή ακόμη και να πέσει. Αυτό οφείλεται στο νόμο του μείωση της οριακής παραγωγικότητας.
Ομοίως, τι σημαίνει εάν το οριακό προϊόν μειώνεται;
Ο νόμος του φθίνουσα οριακή επιστροφές αναφέρει ότι πότε κερδίζεται ένα πλεονέκτημα σε συντελεστή παραγωγή , ο οριακή παραγωγικότητα θα τυπικά ελαττώνω όπως και παραγωγή αυξάνει. Αυτό που σημαίνει ότι το πλεονέκτημα κόστους συνήθως μειώνεται για κάθε επιπλέον μονάδα του παραγωγή που παράγονται.
Στη συνέχεια, το ερώτημα είναι, ποιο είναι ένα παράδειγμα νόμου φθίνουσας απόδοσης; ο νόμος της μείωσης οριακός επιστρέφει δηλώνει ότι, σε κάποιο σημείο, η προσθήκη ενός επιπλέον συντελεστή παραγωγής έχει ως αποτέλεσμα μικρότερες αυξήσεις στην παραγωγή. Για παράδειγμα , ένα εργοστάσιο απασχολεί εργαζόμενους για την κατασκευή των προϊόντων του και, κάποια στιγμή, η εταιρεία λειτουργεί σε βέλτιστο επίπεδο.
Δεύτερον, ποιος είναι ο νόμος του μειούμενου οριακού προϊόντος της εργασίας;
ο νόμος της φθίνουσας οριακής παραγωγικότητας δηλώνει ότι ενώ η αύξηση μιας εισροής και η διατήρηση άλλων εισροών στο ίδιο επίπεδο μπορεί αρχικά να αυξήσει την παραγωγή, περαιτέρω αυξήσεις σε αυτήν την είσοδο θα έχουν περιορισμένη επίδραση και τελικά δεν θα έχουν καμία επίδραση ή αρνητική επίδραση στην παραγωγή.
Τι είναι το οριακό προϊόν με παράδειγμα;
ΕΝΑ οριακό προϊόν είναι η σταδιακή αλλαγή σε παραγωγή αποδίδεται σε μια αλλαγή σε οποιοδήποτε μεμονωμένο στοιχείο εισαγωγής. Για παράδειγμα , οριακό προϊόν μπορεί να είναι ο αυξημένος αριθμός των προϊόντα παράγεται με την προσθήκη ενός επιπλέον εργάτη στο α παραγωγή γραμμή.
Συνιστάται:
Τι είναι Project και προϊόν;

Τα προϊόντα έχουν έναν κύκλο ζωής που αποτελείται από πολλά στάδια. Αρχικά το προϊόν σχεδιάζεται, δεν αναπτύσσεται, στη συνέχεια εισάγεται και διαχειρίζεται στην αγορά, και τέλος το προϊόν αποσύρεται όταν μειώνεται η ανάγκη του. Το Aproject είναι μια προσωρινή προσπάθεια που αναλαμβάνεται για τη δημιουργία ενός μοναδικού προϊόντος ή υπηρεσίας
Όταν το οριακό κόστος είναι πάνω από το μέσο όρο, το συνολικό κόστος πρέπει να μειωθεί;
Όταν το οριακό κόστος είναι κάτω από το μέσο συνολικό κόστος, το μέσο συνολικό κόστος θα μειώνεται και όταν το οριακό κόστος είναι πάνω από το μέσο συνολικό κόστος, το μέσο συνολικό κόστος θα αυξάνεται. Μια εταιρεία είναι πιο παραγωγικά αποδοτική στο χαμηλότερο μέσο συνολικό κόστος, το οποίο είναι επίσης εκεί όπου το μέσο συνολικό κόστος (ATC) = οριακό κόστος (MC)
Πώς υπολογίζεται το οριακό γινόμενο εργασίας του Cobb Douglas;
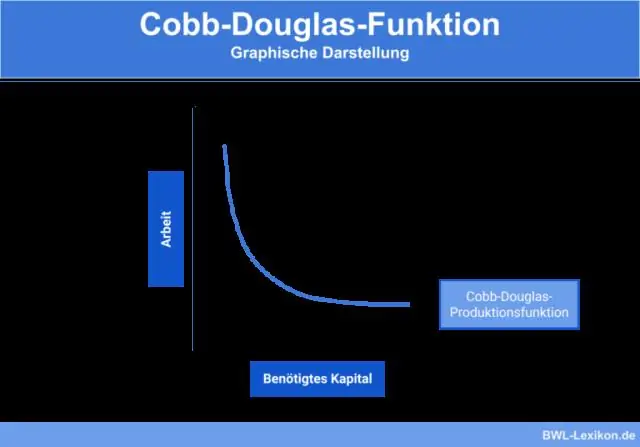
Ας υποθέσουμε ότι Q = f(L, K) είναι η συνάρτηση παραγωγής όπου η παραγόμενη ποσότητα δίνεται ως συνάρτηση της εργασίας και του κεφαλαίου που χρησιμοποιείται. Για παράδειγμα, για τη συνάρτηση παραγωγής Cobb-Douglas Q = f(L, K) = ALa Kb. Για μια δεδομένη ποσότητα εργασίας και κεφαλαίου, ο λόγος Q K είναι η μέση ποσότητα παραγωγής για μια μονάδα κεφαλαίου
Ποιο είναι το οριακό κόστος της μείωσης της ρύπανσης;

Ας αναθεωρήσουμε: Οριακό κόστος ρύπανσης είναι το πρόσθετο περιβαλλοντικό κόστος που προκύπτει λόγω της παραγωγής μιας επιπλέον μονάδας. Το οριακό κόστος μείωσης είναι το κόστος που σχετίζεται με την εξάλειψη μιας μονάδας ρύπανσης. Καθώς η ποσότητα της εκλυόμενης ρύπανσης μειώνεται, το οριακό κόστος μείωσης τείνει να αυξάνεται
Τι υποδηλώνει το οριακό ποσοστό υποκατάστασης MRS μεταξύ σε αγαθά;

Στα οικονομικά, το οριακό ποσοστό υποκατάστασης (MRS) είναι η ποσότητα ενός αγαθού που είναι διατεθειμένος να καταναλώσει ένας καταναλωτής σε σχέση με ένα άλλο αγαθό, εφόσον το νέο αγαθό είναι εξίσου ικανοποιητικό. Χρησιμοποιείται στη θεωρία της αδιαφορίας για την ανάλυση της συμπεριφοράς των καταναλωτών
